1  引言
    伴隨著列車“高速度,、高密度運行”新形勢的飛速發(fā)展，以及全國鐵路6次大提速中出現(xiàn)的“單司機、長交路”等新情況，如何在保證安全的前提下提高鐵路運營管理水平已成為鐵路發(fā)展的當(dāng)務(wù)之急,。為了保證列車的行車安全、提高列車運行效率,，研究列車速度控制并得到滿意的控制效果是非常必要的,。而列車的運行過程是極其復(fù)雜的，不確定因素多且離散性大,。對列車運行過程進行安全有效的控制仍是鐵路自動化領(lǐng)域一直未能很好解決的焦點問題之一。因此關(guān)于列車速度控制方法的研究對鐵路運輸具有十分重要的意義,。然而原有的列車速度控制方法難以滿足安全行車要求,。因此本文采用的預(yù)測控制可以根據(jù)以后的輸入對控制參數(shù)和控制策略進行有計劃的調(diào)整，降低了控制量的時滯,，提高了列車的控制效果和控制效率,。預(yù)測控制利用在線估計預(yù)測模型，減少了由于模型不準確帶來的誤差,，使得模型具有實時性,。由于預(yù)測控制采用在線滾動優(yōu)化指標和反饋校正策略，使系統(tǒng)具有較好的穩(wěn)定性和魯棒性,。

2  列車速度控制數(shù)學(xué)計算模型
2.1 列車的運動方程
    列車是在具有坡道和彎道的軌道上依靠機車的粘著牽引力行駛的,，由于駕駛坡道的長度遠遠大于列車的車長，可將列車作為一個質(zhì)點處理,，其運動方程可用牛頓第二定律表示如下：
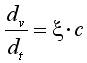                       (1)
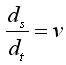                       (2) 
    式中：c—作用于列車上的單位合力(kn),；
          v—列車運行速度(m/s)；
          s—列車走行距離(m),；
    因為單位合力不是常數(shù),，上述方程無法直接求解。試著用逼近法求解：假設(shè)列車在一段很小的計算時間間隔△t內(nèi)單位合力為常數(shù),，可得：
    c =f(v₁,s₁,u₁)－w(v₁,s₁)             (3)
    式中：f(v₁,s₁,u₁),，w(v₁,s₁)分別為在速度v₁、位置s₁,、手柄級位u₁時的總牽引力(包含制動力,，制動力為負)和總阻力。
    因為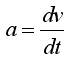加入式可得：
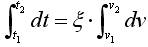                               (4)
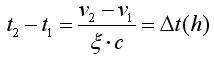                   (5)
    已知v₁,，根據(jù)式(2)近似地求出這一段的c,，根據(jù)式(4)可求出v₂，如此向前推算,，可以畫出列車運行的速度——距離曲線,。其中△t取得越小,，計算精度越高。
2.2 列車制動距離計算
    (1)空走距離
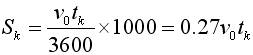               (6) 
    式中：v₀—制動初速,；
          t_k—空走時間,。
    (2)有效制動距離
    用分析法可得分速度間隔的間隔距離為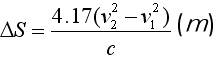：(m)    (7) 
    有效制動距離為：
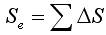       (8) 
    用上式計算有效制動距離時，通常每個速度間隔不超過10km/h,。

3  列車速度控制預(yù)測模型
    假設(shè)在時刻k有u(k)為控制輸入,，s(k)為當(dāng)前位置，v(k)為當(dāng)前速度,。根據(jù)式(2)求得列車的合力c,，根據(jù)式(4)可以確定：
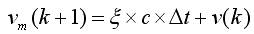               (9) 
    列車運行單步輸出預(yù)測模型為：
    v_m(k+1)=g(v(k), u(k), s(k))        (10) 
    式中：g(v(k), u(k), s(k))為函數(shù)表達式，表明vm(k+1)是v(k), u(k), s(k)的合成函數(shù),。由式(9)遞推疊代的方法可以得到列車多步的運行速度輸出預(yù)測公式：    
    v_m(k+p△t) = g(v(k+(p－1)△t),…,v(k+(p－(p－1)△t)),v(k), u(k), s(k) (11)
    式中：p—預(yù)測步數(shù),；
        △t—采樣時間。
    根據(jù)預(yù)測模型引入實際模型與預(yù)測模型當(dāng)前輸出之間的偏差進行修正,，修正后的1步預(yù)測輸出為：
    v_p(k+1)= v_m(k+1)+h(v(k)－v_m(k))
           = v_m(k+1)+ he(k)           (12)
    其中：e(k)—實際模型和預(yù)測模型k時刻的誤差,；
             h—誤差修正系數(shù)。
    我們可確定預(yù)測誤差的目標函數(shù)為：
    j_p=[v_p(k+1)－v (k+1)]²           (13) 
    取滾動優(yōu)化中的優(yōu)化性能指標為：
    j_p=[v_p(k+1)－v (k+1)]²             (14)
    根據(jù)優(yōu)化性能指標求取最優(yōu)控制量：
    令 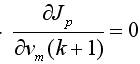        (15)
    得v_m(k+1)+he(k)－v(k+1)=0     (16)
    即v_m(k+1)= v(k+1)－h(huán)e(k)        (17)
    這里 v_m(k+1)=△u(k)                (18)
    所以,，最優(yōu)控制變化量為：
      △u(k)=v(k)+he(k)                  (19)

4  列車速度預(yù)測控制算法
    列車速度預(yù)測控制過程示意圖如圖1所示,。系統(tǒng)的控制過程以一個閉塞區(qū)間為單位進行。圖中v_in為列車的入口速度,；v_out為列車運行出口速度,；s(k)為制動區(qū)，它是由預(yù)測模型根據(jù)線路條件,、入口/出口速度,，以標稱減壓量計算出來的；s(k+α△t)為一個控制時間α△t(α為控制時間常數(shù))內(nèi)的列車運行距離,；s_max為實施上一個控制時間后,，由預(yù)測模型計算出來的余下運行時間內(nèi)的列車制動距離?！鱯為安全防護距離(貨車為100m,，客車40m)。這里的標稱減壓量隨著速度的高低有所不同,。

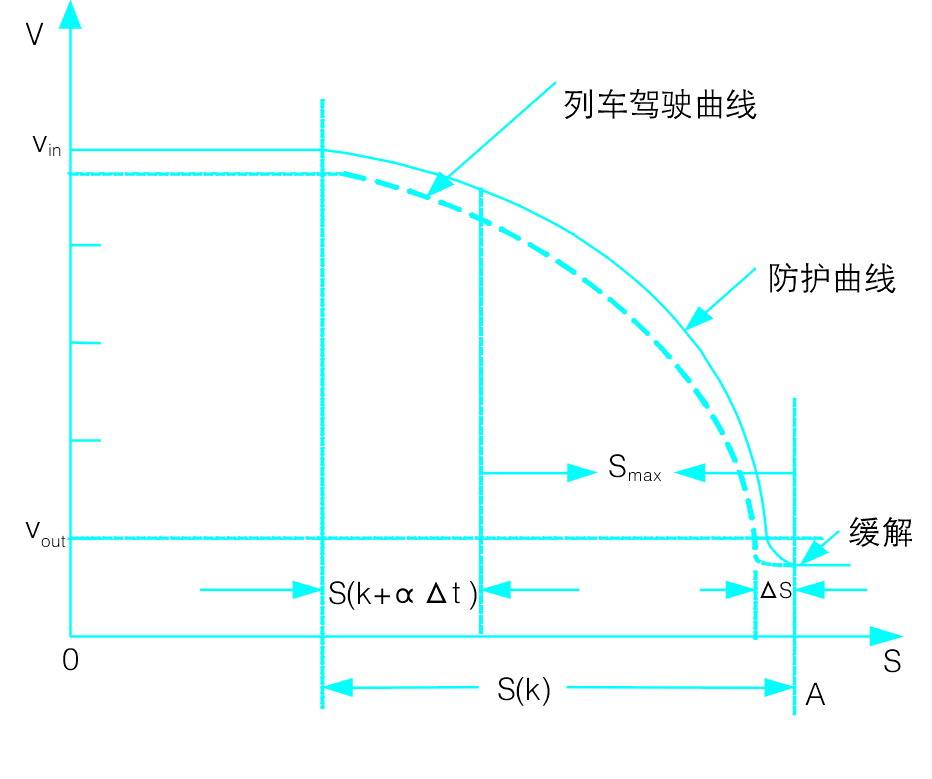
圖1  速度預(yù)測控制過程示意圖

5  仿真實驗與結(jié)果分析
    以蘭州-定西鐵路線路為實驗線路,，選取駱駝巷-桑園子一個閉塞區(qū)間研究列車的速度預(yù)測控制并進行系統(tǒng)仿真。線路具體參數(shù)如下：線路全長1.9km,，最高限速為100km/h,，允許速度為60km/h，限制慢行速度為30km/h，平均坡度為6‰,，曲線半徑為r680,。機車型號為ss3b型，載重4000t,，編組50輛,，列車管壓500kpa，采用高磷閘瓦,。
    根據(jù)列車運行特點,，利用預(yù)測控制方法對列車運行速度設(shè)計仿真程序，利用matlab軟件仿真,。仿真結(jié)果如圖2,、圖3、圖4所示,。

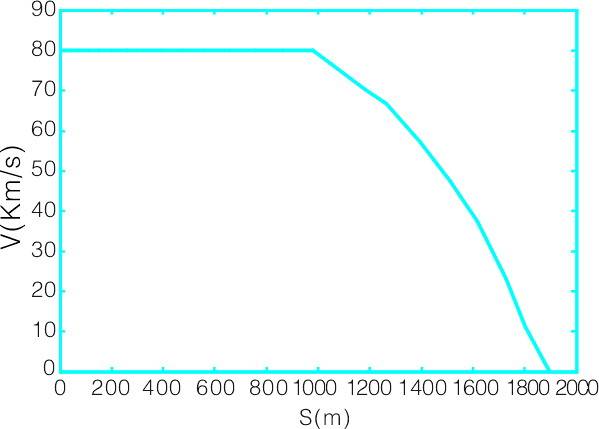
圖2  列車常規(guī)制動速度-距離控制曲線

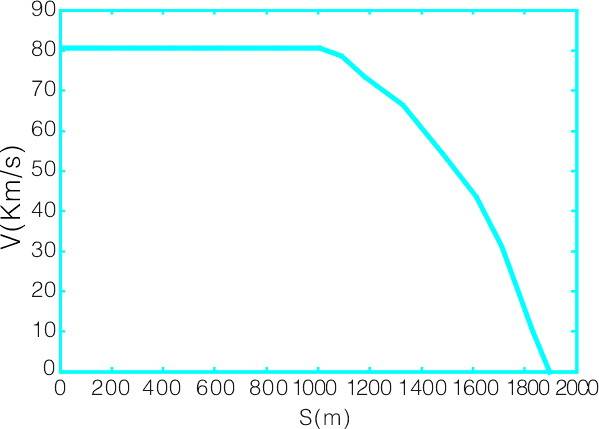
圖3  基于預(yù)測控制的列車速度-距離曲線

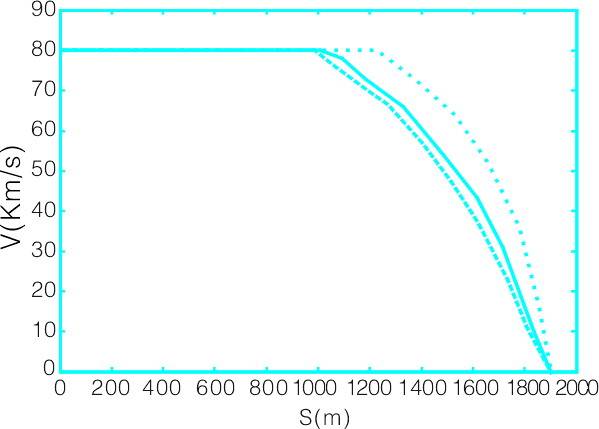
圖4  同車同速,、不同控制方法制動曲線圖

    列車速度控制曲線如圖2所示。列車在979.2m開始實施制動,，在此之前進行速度為80km/h的勻速運動。然后列車開始進行加速度不等的減速運動,。列車在1.9km處速度為0,。
    列車速度預(yù)測控制曲線如圖3所示。列車在距列車在1030m開始實施制動,，在此之前進行速度為80km/h的勻速運動,。因為列車的阻力與列車速度有關(guān)，所以在不同速度時刻列車的阻力不同,，列車的加速度也不同,，列車運行是一變槳加速度運動。列車在1.9km處速度為0,。圖中橫坐標為列車運行預(yù)測控制的距離,，縱坐標為列車運行速度。
    圖4為同車同速,、不同控制方法制動曲線圖,。圖中橫坐標為列車運行控制的距離，縱坐標為列車運行速度,。預(yù)測控制列車速度在制動過程中小于防護速度,，大于列車常規(guī)制動速度。說明列車速度預(yù)測控制方法優(yōu)于常規(guī)制動,。

作者簡介
    邱亞娟(1983-)  女  碩士研究生,，研究方向為伺服電機控制技術(shù)。

參考文獻 (略)